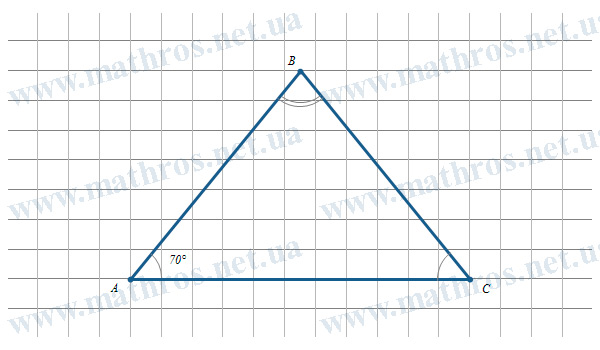
- Як знайти суму внутрішніх кутів трикутника: від теорії до практики
- Основи геометрії: трикутники і їх значення
- Властивості трикутників
- Алгоритм підрахунку: як знайти ці 180 градусів?
- Крок за кроком
- Практичні приклади та задачі
- Приклад 1: Рівносторонній трикутник
- Приклад 2: Прямокутний трикутник
- Трикутники в реальному житті: де і як?
- Чи є винятки? Інші погляди на трикутники
- Висновки: важливість знання сум кутів
Як знайти суму внутрішніх кутів трикутника: від теорії до практики
Як знайти суму внутрішніх кутів трикутника? Це просте, але фундаментальне питання. Відповідь на нього може виявитися корисною не тільки для школярів, але і для тих, хто цікавиться основами геометрії. Поговоримо про внутрішні кути, їх властивості та як точно визначити їх суму.
Уявіть собі трикутник: тричастинний геометричний об’єкт, що має свою таємницю у вигляді суми своїх внутрішніх кутів. Спочатку здається, що це зовсім неважливо, але якщо задуматись, трикутник — це взагалі фундаментальна фігура. Вона формує основу багатьох інших багатокутників, тому варто зрозуміти, як працюють його внутрішні кути.
Основи геометрії: трикутники і їх значення
Геометрія — така штука, що їй вже кілька тисяч років. І попри свій поважний вік, вона продовжує бути актуальною. Трикутники, цей замкнутий двовимірний об’єкт з трьома кутами і трьома сторонами, лежить в основі всіх багатокутників. Як гадаєте, скільки часу людство витратило на вивчення лише цієї фігури?
Отже, основи. Доведено, що сума внутрішніх кутів трикутника завжди становить 180 градусів. Хочеш трикутник більший, менший, ширококутний або тісний, але всередині нього завжди буде 180 градусів. Це як правило гри, що не змінюється.
Властивості трикутників
- Равнобедрений трикутник має дві рівні сторони, а відповідно, і два рівних кута.
- Рівносторонній трикутник має всі сторони й кути рівні. Кожен кут — по 60 градусів.
- Прямокутний трикутник: один з його кутів завжди дорівнює 90 градусів.
Алгоритм підрахунку: як знайти ці 180 градусів?
Чесно, це не так вже й складно. Згадайте школу: щоб зрозуміти, яка сума внутрішніх кутів трикутника, треба лише знати властивості та основні формули. Є кілька способів дійти до істини, давайте їх розглянемо.
Крок за кроком
- Спочатку виміряйте два з трьох кутів трикутника в градусах.
- Додайте отримані значення.
- Відніміть цю суму від 180 градусів. Це і буде величина невідомого кута.
Практичні приклади та задачі
Бажаєте трохи практики? Адже теорія без практики — це як холодний чай. Отож, розглянемо кілька прикладів, що допоможуть глибше зрозуміти, чому 180 градусів не є випадковістю.
Приклад 1: Рівносторонній трикутник
| Кут 1 | Кут 2 | Кут 3 | Сума |
|---|---|---|---|
| 60° | 60° | 60° | 180° |
Як бачите, кожен кут дорівнює 60 градусів. І сумарно — 180 градусів. Ідеальна гармонія, чи не так?
Приклад 2: Прямокутний трикутник
Уявіть трикутник, де один кут дорівнює 90 градусів. Для прямокутного трикутника легко вибрати інші два. Пам’ятайте про те ж саме правило: всі разом дають 180 градусів.
Трикутники в реальному житті: де і як?
І чому трикутник? Здавалося б, є купа інших геометричних фігур. Вдома, на вулиці, в архітектурі — трикутники скрізь. Чому їх так багато? Все справді просто. Трикутники надійні та стабільні, їх використовують в конструкціях, щоб забезпечити міцність і надійність.
Наприклад, конструкція моста часто включає трикутні елементи. Ще й каркаси дахів будинків — це суцільна трикутність. Вони не тільки гарні на ефективні.
Чи є винятки? Інші погляди на трикутники
А іноді, наш світ перевертається з ніг на голову. У геометрії існує так звані неевклідові системи, де рівняння для трикутників можуть бути трохи іншими. Але це вже історія для інсайдерів геометрії.
І все-таки, залишаймося простими. У базовій геометрії на площині трикутник завжди видає нам свої 180 градусів. Ось така магія чисел при дуже простих умовах.
Висновки: важливість знання сум кутів
На перший погляд можна не завжди зрозуміти, чому знання про суми внутрішніх кутів трикутника настільки важливі. Але варто замислитися, і ви побачите як таке, здавалося б, маленьке знання може відчинити двері до багатьох розумінь і відкриттів. Секрет у простоті, в елегантності таких пошуків.
Знайти суму внутрішніх кутів трикутника — це один з фундаментальних аспектів, які привносять глибину у розуміння геометрії. І якщо бути уважним, це знання може вас здивувати та надихнути на нові дослідження.