Що таке аксіома: Основи, визначення та роль у логіці та математиці

Що таке аксіома: основи логіки та математики

Що таке аксіома? Це просте питання відкриває величезний світ фундаментальних істин, які приймаються без доказів. Аксіома служить ключовою відправною точкою в побудові теорій — від математики до філософії. Саме вона визначає базис, на якому творяться інші твердження і докази. У математичних системах аксіоми є основою для таких грандіозних структур, як евклідова геометрія або теорія множин.

Історія аксіом

Витоки концепції

Концепт «аксіоми» вперше отримав офіційне визнання ще у стародавній Греції. Там грецький філософ Арістотель заклав основи логічного мислення у своїх працях — і своєрідно систематизував аксіоми. Тим не менше, саме Евклід, давньогрецький математик, який у своїх знаменитих «Началах» сформулював аксіоми для евклідової геометрії, додав цьому підвалину видатної геометричної доктрини.

Роль аксіом у математиці

Математичні системи

Аксіоми виступають основним дійовим інструментом у конструюванні математичних систем. Вони диктують ключові властивості і взаємовідношення об’єктів. У евклідовій геометрії, наприклад, аксіоми визначають властивості, притаманні точкам, прямим і площам. Аналогічно, аксіоми теорії множин встановлюють основні правила при роботі з множинами, а аксіоми арифметики визначають корінні ознаки чисел.

Приклади аксіом

Евклідові аксіоми

Евклід запропонував п’ять основних аксіом для геометрії:

1. Через будь-які дві точки проходить єдина пряма.
2. Пряму дозволено продовжити невизначено в обидва боки.
3. З будь-якого центру можна описати коло будь-яким радіусом.
4. Всі прямі кути за визначенням рівні.
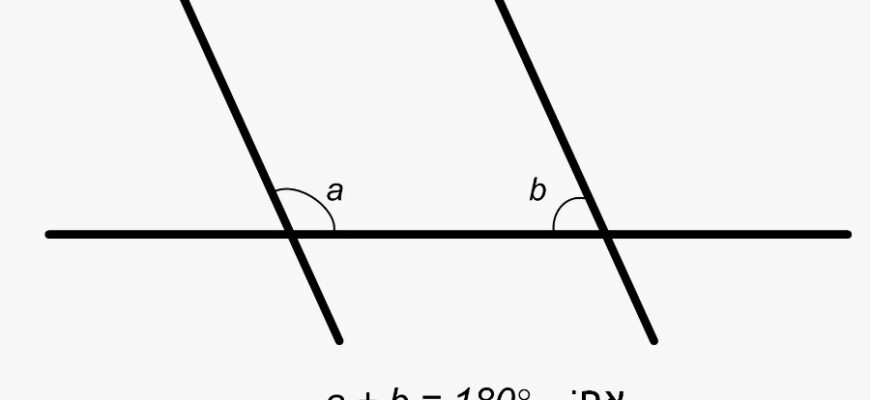
5. Якщо одна пряма перетинає дві інші так, що сума внутрішніх кутів з одного боку менша ніж два прямих кути, то ці дві прямі, якщо їх продовжити, обов’язково перетнуться з того ж боку.

Аксіоми Пеано

Аксіоми Джузеппе Пеано формують фундус для натуральних чисел і включають:

1. Існує початкове натуральне число 0.
2. Кожне натуральне число має наступника.
3. Число 0 не є наступником жодного іншого числа.
4. Рівність наступників достатня для рівності чисел.
5. Якщо всі числа мають певну властивість після 0 і наступнику будь-якого числа, то ця властивість належить всім натуральним числам.

Важливість аксіом у логіці

Логічні системи

В основі створення логічних систем є аксіоми. Саме вони визначають базові правила та принципи, за якими робляться висновки. Завдяки їм створюються формальні системи, де аналіз аргументів і доведення тверджень оптимізовано до межі можливого.

Формальні системи

У таких структурах, як логіка першого порядку, аксіоми служать вихідними твердженнями, з яких за допомогою правил виводу розгортаються інші судження. Це створює можливість втримати теорії в формалізованих межах, надавши обробленню доводів максимальної строгості.

Виклики та обмеження аксіом

Незалежність аксіом

Незалежність аксіом має значення тільки тоді, коли одна не може бути виведена з інших. Це показує, що кожна аксіома додає щось нове. Незалежність — це своєрідна вільність в межах правил, яку сприймати як належне не так просто, як здається.

Неповнота

Незважаючи на їх вагомість, аксіоми обмежені. Наприклад, теореми неповноти Геделя вказують, що в будь-якій достатньо потужній формальній системі, такій, яка охоплює арифметику, завжди існують твердження, що як не крути — не можуть бути доведені або спростовані на основі системних аксіом.

Список основних понять про аксіому

• Аксіома: Фундаментальний принцип без доказів.
• Евклідові аксіоми: П’ять аксіом евклідової геометрії.
• Аксіоми Пеано: Збірник аксіом натуральних чисел.
• Незалежність аксіом: Жодну з аксіом не можна вивести з інших.
• Неповнота: Існування тверджень, що не довідні чи спростовні.
• Логічні системи: Формальні системи для доведення теорем.
• Формальні системи: Структуровані настанови для аналізу.
• Арістотель: Філософ, що систематизував аксіоми.
• Евклід: Математик, що сформулював аксіоми геометрії.
• Теореми неповноти Геделя: Обмеження аксіоматичних систем.

І завершити потрібно важливим нагадуванням: аксіоми — це не просто формальні принципи; вони є стрижнем усього логічного та математичного мислення. Аксіоми служать орієнтирами для доведення теорем та розвитку теорій. Вони потрібні для формалізації знань і аналізу систем. За розумінням аксіом стоїть необхідність усвідомлення логіки та математики, а їх значимість у науці та філософії важлива як ніколи.